Les tables de hachage

On peut distinguer deux types de tables de symboles : les tables associatives (maps en anglais) et les dictionnaires. Ce sont exactement les mêmes structures avec une légère différence (mais de taille !) : les clés des maps sont uniques tandis que celles d'un dictionnaire ne le sont pas nécessairement. Cela peut paraître anodin, mais en pratique, c'est très important.

Ainsi, le répertoire téléphonique est un dictionnaire : vous pourriez très bien avoir deux contacts qui portent le même nom, mais qui ont des numéros différents. Ou bien vous pourriez associer à une même personne plusieurs numéros, par exemple son téléphone fixe et son téléphone portable. Un dictionnaire est également un… dictionnaire puisque certains mots peuvent avoir plusieurs significations.
À l'opposé, l'unicité des id des news d'un site est primordiale ; imaginez que deux news possèdent le même id, comment savoir laquelle consulter ?

Définissons à présent le type de donnée abstrait d'une table de symboles, autrement dit ce que l'on peut faire avec ; on a les méthodes suivantes :

• put(clé, valeur) : permet d'ajouter une paire « clé-valeur » ;
• get(clé) : comme son nom l'indique, retourne la valeur associée à une clé ;
• remove(clé) : je ne vous le cache pas plus longtemps, supprime une paire ;
• contains(clé) : retourne vrai si la clé se trouve dans la table, faux sinon ;
• size() : retourne le nombre de paires entrées dans la table ;
• isEmpty() : retourne vrai si la table est vide, faux sinon.

Voici l'interface Java que nous nous amuserons à implémenter par la suite :

public interface SymbolTable <K, V>
{
    public void put(K key, V value) throws HashTableException;
    public V get(K key) throws HashTableException;
    public V remove(K key) throws HashTableException;
    public boolean contains(K key) throws HashTableException;
    public int size();
    public boolean isEmpty();
}

Les exceptions sont là « pour faire propre ». Si vous reprenez cette interface, vous n'êtes pas obligé de les utiliser (même si cela reste plus élégant que de renvoyer des valeurs particulières). Pour ceux que cela intéresse, voici le code Java de cette exception.

public class HashTableException extends Exception
{
    public HashTableException()         { super() ; }
    public HashTableException(String s) { super(s); }
}

Il existe plusieurs manières d'implémenter ces méthodes. On peut notamment citer

• un tableau ;
• une liste ;
• un arbre (BST, AVL, etc.) ;
• une table de hachage.

Les tableaux et les listes peuvent être utilisés avec deux variantes (les clés sont triées ou non), qui sont efficaces avec certaines méthodes et pas du tout avec d'autres : il faut choisir entre la peste et le choléra. Retenez que ces implémentations ne sont pas optimales et à éviter à tout prix.
Restent les arbres et les tables de hachage, qui ont aussi leurs avantages et inconvénients ; nous en rediscuterons lorsqu'on se penchera sur les performances, à la fin de la partie théorique de cet article. En résumé, on aura les complexités temporelles suivantes.

Les complexités des tables de hachage peuvent paraître miraculeuses, mais nous verrons que tout n'est pas rose pour autant. Retenez que les tableaux et les files sont très inefficaces pour implémenter les tables de symboles, et que les arbres et tables de hachage sont les solutions les plus efficaces.

Partout où vous aurez besoin de stocker des données, vous aurez besoin de tables de symboles, et un choix cornélien à faire entre les arbres et les tables de hachage. Ces dernières sont utilisées dans beaucoup de situations pratiques :

• les array du langage PHP sont implémentés avec des tables de hachage, merci à doctorrock pour l'info (pour les plus curieux, voici le code source) ;
• dans un compilateur, on les emploie généralement pour stocker des mots-clés et les variables utilisées. Ainsi, si dans le code on utilise une variable, on peut vérifier très rapidement si elle a été déclarée auparavant (si c'est nécessaire bien sûr) ;
• dans un correcteur orthographique, on utilise des tries pour stocker les mots d'un dictionnaire, mais pour vérifier si un mot est correctement écrit, le parcours se fait en kitxmlcodeinlinelatexdvp\mathcal{O}(L)finkitxmlcodeinlinelatexdvp (avec L la longueur du mot). Pour gagner de la vitesse, vous pouvez stocker les mots du dictionnaire dans une table de hachage. Ainsi pour vérifier si le mot est correctement orthographié ou non, le temps sera constant ;
• les arbres et les tables de hachage sont utilisés dans les bases de données, généralement et respectivement pour stocker lesdites données et pour stocker des relations temporaires ;
• etc.

Les tables de hachage sont disponibles par défaut dans plusieurs langages, comme en PHP, en Java, en Perl ou encore en PowerShell. N'hésitez pas à faire un tour dans la documentation de votre langage préféré afin de ne pas les réimplémenter pour rien.

Pour faire simple, le hash code d'un objet ou d'une variable est un entier qui lui est associé et qui est idéalement propre à chaque élément. C'est le résultat d'une fonction de hachage, on dit qu'elle hache l'élément.

On pourrait faire tout un cours sur les fonctions de hachage, mais pour rester simple une bonne fonction de hachage (que l'on va appeler kitxmlcodeinlinelatexdvph_hfinkitxmlcodeinlinelatexdvp dans le reste de cet article) doit respecter les deux conditions suivantes :

1. si deux clés sont identiques, leur hachage l'est aussi ; en d'autres mots, pour deux clés kitxmlcodeinlinelatexdvpk_1finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpk_2finkitxmlcodeinlinelatexdvp, si kitxmlcodeinlinelatexdvpk_1 = k_2finkitxmlcodeinlinelatexdvp alors kitxmlcodeinlinelatexdvph_h(k_1) = h_h(k_2)finkitxmlcodeinlinelatexdvp ;
2. les hash codes doivent être tous uniques ; si kitxmlcodeinlinelatexdvpk_1 \neq k_2finkitxmlcodeinlinelatexdvp , alors kitxmlcodeinlinelatexdvph_h(k_1) \neq h_h(k_2)finkitxmlcodeinlinelatexdvp.

La première condition est obligatoire, mais est relativement facile à faire respecter, tandis que la seconde est beaucoup plus difficile à mettre en pratique (surtout dans le cas des tables de hachage).

En effet, les tables de hachage utilisent le hash code pour placer une paire dans un tableau, mais ce code peut potentiellement prendre n'importe quelle valeur (théoriquement de kitxmlcodeinlinelatexdvp- \inftyfinkitxmlcodeinlinelatexdvp à kitxmlcodeinlinelatexdvp+ \inftyfinkitxmlcodeinlinelatexdvp, mais on sera ici limité par le type de donnée que l'on utilisera). Il va donc falloir le compresser, c'est-à-dire le borner aux indices du tableau. On appliquera pour cela une fonction de compression (que l'on va ici noter kitxmlcodeinlinelatexdvph_cfinkitxmlcodeinlinelatexdvp). Ainsi, l'indice d'un élément i, qui sera donné par la fonction kitxmlcodeinlinelatexdvphfinkitxmlcodeinlinelatexdvp, est défini comme suit :

Par exemple, imaginons que nous ajoutons le numéro de téléphone Jean-Paul Belmondo. L'ajout se déroulera selon le schéma ci-dessous.

Illustrons le mécanisme que nous allons implémenter avec un petit exemple numérique, cela ne sera pas de trop. Imaginons que l'on dispose des fonctions suivantes :

On aimerait insérer les clés suivantes dans un tableau de 10 cases (les valeurs associées ici n'ont pas beaucoup d'importance, on va les laisser de côté) : 0, 4, 7 et 42 (soyons fous). En sortant la calculette, on obtient les résultats ci-dessous :

Et si on place les clés dans un tableau, on a

Diablement simple, n'est-il pas ?

I-D-1-a. Le principe▲

Appelé linear probing en anglais, le sondage linéaire est une idée très intuitive : si on a une collision, à partir de l'indice, on parcourt le tableau jusqu'à trouver une case libre. Les indices parcourus peuvent être écrits sous la forme suivante, avec M la taille du tableau, kitxmlcodeinlinelatexdvphfinkitxmlcodeinlinelatexdvp la fonction de hachage-compression, et i un indice qui varie de 0 à M :

kitxmlcodelatexdvp\text{indice} = (h(k) + i) \mod Mfinkitxmlcodelatexdvp

Ainsi, pour placer 22, vu que la case à l'indice 0 est occupée, on va vérifier en 1. C'est vide, on l'y insère !

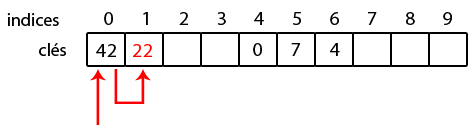
Ajoutons la clé 30 ; on a kitxmlcodeinlinelatexdvph_h(30) = 104finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvph_c(h_h(30)) = 4finkitxmlcodeinlinelatexdvp. La case 4 est occupée, on parcourt alors les indices jusqu'à trouver une case libre. La première case libre est en 7, on y met 30 !

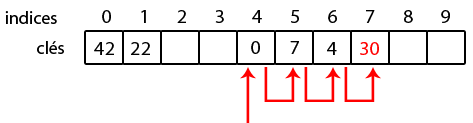
C'était pour l'insertion d'une clé. La recherche fonctionne sur le même principe : on va calculer l'indice de la clé qu'on cherche avec la fonction de hachage. Ensuite, tant qu'on n'a pas trouvé la clé, on descend dans le tableau. Si on tombe sur une case vide ou si on a parcouru toutes les cases (cas d'une table pleine), c'est que la clé n'est pas dans la table.

Par exemple, si on cherche la clé 62, on va calculer son indice qui vaut 0. Puisque la clé en 0 n'est pas celle qu'on cherche, on va continuer et tester les indices 1 et 2. Vu que la case 2 est vide, la clé n'est pas dans la table, sinon on l'aurait nécessairement trouvée.

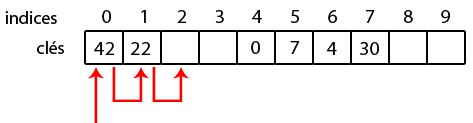
I-D-1-b. Une petite subtilité : la suppression▲

L'insertion de clés est relativement simple, mais c'est la suppression qui est délicate et qui peut rendre la table de hachage inconsistante. Comme dit plus haut, on va descendre dans le tableau jusqu'à trouver la clé ou une case vide… Si la suppression rend une case vide sur le « chemin » à parcourir, alors on perdra l'accès à certaines clés !
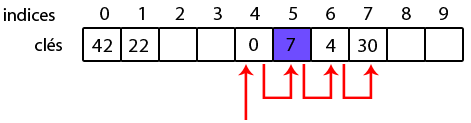
Par exemple, imaginons qu'on supprime purement et simplement la clé 7 qui est à l'indice 5, après avoir inséré la clé 30.

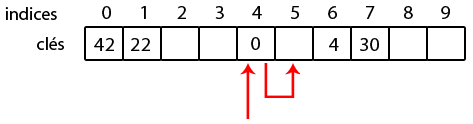
Dès lors, on ne saura jamais trouver 30 vu que le « chemin » pour y accéder passe par une case vide, sur laquelle le programme va s'arrêter.
Une solution simple pour éviter ces pertes est, lorsqu'on demande la suppression d'une clé, de la garder, mais de marquer la case comme libre. Ainsi, lorsqu'on cherchera 30, on passera dessus sans problèmes. Il faut juste penser, dans la méthode pour ajouter une paire « clé-valeur », à chercher la première case vide ou marquée libre. Il faudra aussi y penser lors de la recherche d'une clé : il faudra chercher la clé et, si on la trouve, vérifier que la case n'est pas libre. En effet, si elle est libre, c'est que la clé a été supprimée.

I-D-1-c. Avantages et inconvénients▲

Le système de sondage est simple dans son fonctionnement et son implémentation, mais malheureusement souffre d'un problème de clustering. En fait, les clés vont avoir tendance à s'agglutiner, à former des grappes dans le tableau. Le souci surviendra quand il faudra parcourir toute la grappe pour trouver une case disponible ou une clé ; le temps d'exécution grimpera en flèche !

L'exemple de tout à l'heure illustre ce phénomène : pour ajouter 30, il a fallu faire 4 tests pour trouver sa place définitive. Dans ce cas-ci c'est peu. Mais avec des tableaux de centaines de milliers, voire de millions d'éléments, il faudra prendre patience ! Une manière d'éviter ces grappes consiste à utiliser un sondage d'un degré plus haut (comme nous allons le voir par la suite). Des clusters existeront toujours, mais seront plus petits.
Sachez aussi que les temps de recherche seront potentiellement plus grands lorsque le tableau se remplit. Ainsi, le tableau ci-dessous montre le pire des cas que vous pourriez rencontrer lorsqu'on insère 38.

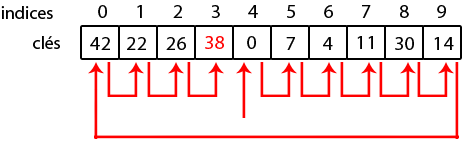
En clair, un sondage linéaire est une manière très efficace de gérer les collisions si le tableau n'est pas trop rempli.

Un moyen d'éviter le clustering du sondage linéaire est d'utiliser un sondage quadratique : le principe est exactement le même, c'est la forme des indices qui change ; si kitxmlcodeinlinelatexdvpc_1finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpc_2finkitxmlcodeinlinelatexdvp sont des constantes (et où kitxmlcodeinlinelatexdvpc_2finkitxmlcodeinlinelatexdvp est non nulle),

Reprenons notre exemple de tout à l'heure, avec kitxmlcodeinlinelatexdvpc_1finkitxmlcodeinlinelatexdvp valant 0 et kitxmlcodeinlinelatexdvpc_2finkitxmlcodeinlinelatexdvp valant 1. Si on insère 22 (dont le hash code est 0), on testera les indices 0 et 1. Pour insérer 30, on ira d'abord voir en 4, puis en 5 et enfin en 8.

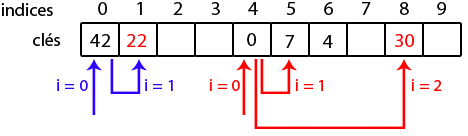
Le sondage quadratique fonctionne beaucoup mieux que le sondage linéaire, la formation de grappes y étant moindre. Ainsi, dans l'exemple, la clé 30 ne rejoint pas la grappe formée par 0, 7 et 4.
En revanche, les problèmes vont se manifester lorsqu'on aura deux clés dont le hash code est le même. En effet, elles vont toutes les deux emprunter le même chemin. Par exemple, si pour une clé le hash code vaut 4, comme dans le cas de la clé 30 il va falloir passer par les indices 4, 5 et 8 avant d'arriver à 3 !

En cas de collision dans un sondage quadratique, on dit que les clés vont former des grappes secondaires. Elles sont moins importantes que les grappes du sondage linéaire, car elles sont plus éparpillées, mais restent problématiques.

I-D-3-a. Le principe▲

L'idée du double hachage est similaire à celle du sondage : on va chercher la première case disponible en faisant varier un indice i, mais en plus de l'incrémenter, on va y inclure un second hachage de la clé ! Ainsi, cela évitera du clustering (en supposant bien sûr que la fonction de hachage soit correcte).
Si on prend comme seconde fonction de hachage kitxmlcodeinlinelatexdvph_2finkitxmlcodeinlinelatexdvp, les indices testés auront la forme :

kitxmlcodelatexdvp\text{indice} = (h(k) + ih_2(k)) \mod Mfinkitxmlcodelatexdvp

Comme exemple, on va insérer 22 et 30 avec la fonction kitxmlcodeinlinelatexdvph_2finkitxmlcodeinlinelatexdvp définie de cette manière :

kitxmlcodelatexdvph_2(i) = 2 \times i + 5finkitxmlcodelatexdvp

Ainsi, si on insère la clé 22 dont le hash compressé principal est 0 et dont le hash secondaire est 49 :

• i = 0, l'indice est kitxmlcodeinlinelatexdvp0 + 0 \times 49 \mod 10 = 0finkitxmlcodeinlinelatexdvp, qui est occupé ;
• i = 1, l'indice est kitxmlcodeinlinelatexdvp0 + 1 \times 49 \mod 10 = 9finkitxmlcodeinlinelatexdvp, qui n'est pas occupé, on doit s'arrêter.

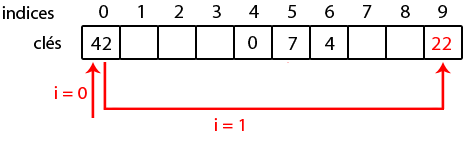
Cette méthode peut paraître séduisante, mais peut rapidement dégénérer. Par exemple, ajoutons 30 : son hash primaire est 4 et son hash secondaire est 65. On a ainsi

• i = 0, l'indice est 4 qui est occupé ;
• i = 1, l'indice est kitxmlcodeinlinelatexdvp(4 + 1 \times 65) \mod 10 = 9finkitxmlcodeinlinelatexdvp, qui est occupé ;
• i = 2, l'indice est kitxmlcodeinlinelatexdvp(4 + 2 \times 65) \mod 10 = 4finkitxmlcodeinlinelatexdvp, qui est occupé ;
• i = 3, l'indice est kitxmlcodeinlinelatexdvp(4 + 3 \times 65) \mod 10 = 9finkitxmlcodeinlinelatexdvp, qui est occupé ;
• etc.

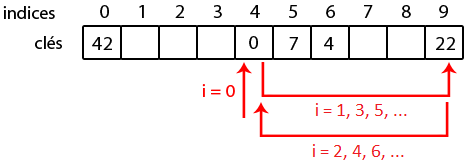
Bref, on tourne en rond, et c'est un des risques de la méthode du double hachage : si on ne fait pas attention, il se peut qu'on ne trouve jamais une case libre (alors qu'on n'en manque pas). Ici, le problème est que la taille du tableau et le hash code sont des multiples de 5.

I-D-3-b. Avantages et inconvénients▲

I-D-4-a. Le principe▲

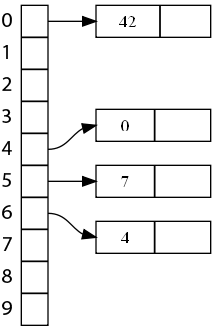
Clôturons ce rapide tour d'horizon des méthodes de gestion des collisions avec le chaînage linéaire ! Il utilise un stratagème tout à fait différent, mais pas plus difficile à comprendre : au lieu d'avoir un élément par bucket, on va avoir une liste. Lorsqu'on place un élément dans le bucket, on l'ajoute dans la liste, et quand il y a une collision… on l'ajoute aussi dans la liste ! Un dessin sera plus explicite : voici la table de notre exemple :

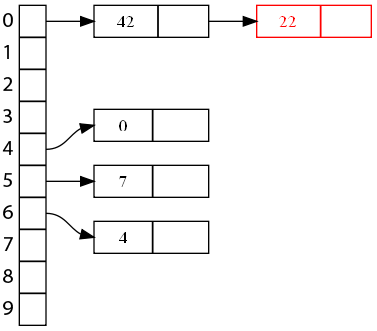
Et maintenant, voici ce qui se passe avec l'insertion de la clé 22.

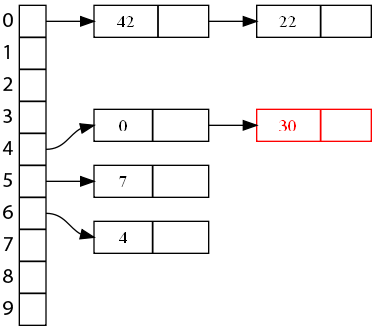
Continuons avec une autre clé qui posait problème, 30.

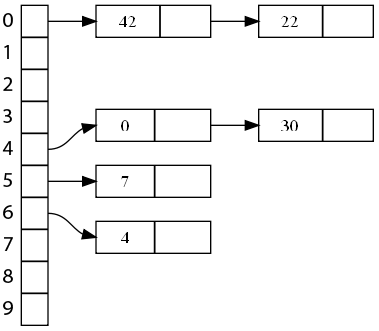
Donc pour ajouter une clé, il suffit de l'ajouter dans la liste. Pour chercher une clé, il suffit de parcourir la liste de l'indice qui lui est associé. Enfin, pour supprimer une clé, on supprime simplement un nœud de la liste de l'indice concerné. Simple et efficace, qui plus est !

I-D-4-b. Avantages et inconvénients▲

Rappelez-vous que, dans notre table de hachage, les indices sont générés en deux opérations :

• le hachage : on hache la clé, qui donne un nombre pouvant être très grand en valeur absolue ;
• la compression : on compresse le hash code, pour qu'il puisse rentrer dans la table.

Comme nous allons le voir un peu plus bas, il est assez « facile » d'avoir une bonne fonction de hachage, les problèmes apparaissent dans la compression.

Pour que cette dernière soit efficace, la première chose qu'elle devra faire est de satisfaire l'hypothèse de hachage uniforme simple, qui dit que chaque clé a la même chance d'être placée dans une case que dans n'importe quel autre emplacement de la table, indépendamment des endroits où les autres clés sont allées.
Autrement dit, lors de l'ajout d'une clé, pour une case quelconque d'une table de taille M, il y a une chance sur M pour que la clé se trouve dans cette case.

Malheureusement, il est très difficile de trouver LA fonction qui vérifie cette condition sans avoir des informations précises sur les clés. Cependant, il est possible d'avoir une compression très efficace et sûre avec les fonctions qui suivent.

I-E-2-a. Hachage polynomial▲

public int hash(String s)
{
    int h = 0;
    
    // Étape 1 - Hachage
    for(int i = 0 ; i < s.length() ; i++) // On parcourt tous les caractères
        h += (int) s.charAt(i);
}

public int hash(String s)
{
    int h = 0;
    int c = 42;
    // Étape 1 - Hachage
    for(int i = 0 ; i < s.length() ; i++) // On parcourt tous les caractères
        h += (int) s.charAt(i) * (int)(Math.pow(c, i));
}

I-E-2-b. Hachage cyclique▲

public int hash(String s)
{
    int h = 0;

    // Étape 1 - hachage
    for(int i = 0 ; i < s.length() ; i++) // On parcourt tous les caractères
    {
        h = (h << 5) | (h >>> 27); // Décalage cyclique de 5 bits
        h += (int) s.charAt(i);
    }
}

I-E-3-a. Méthode de la division▲

public int hash(String s)
{
    int h = 0;

    // Étape 1 - hachage
    // ...
    
    // Étape 2 - compression
    return abs(h) % bucketArray.length;
}

private int hash(String s)
{
    // ...
    return (abs(h) % p) % bucketArray.length;    
}

I-E-3-b. Méthode de la multiplication▲

private double c = 0.618;

private static int hash(String s)
{
    // ...                
    return floor(m * ( ( (double) abs(h) * c) % 1)) ;
}

Malheureusement, nous ne vivons pas dans un monde où tout est rose, et il peut arriver qu'un adversaire cherche à vous mettre des bâtons dans les roues. Les fonctions que nous avons vues auparavant ont le désavantage d'être déterministes : quand vous hachez et compressez deux fois la même clé, l'indice sera le même.
Ainsi, sans protection, l'adversaire pourrait s'amuser à entrer des clés qui créent de nombreuses collisions, et rendre totalement inefficace la table de hachage. Il pourrait faire complètement dégénérer la situation avec plusieurs tables de hachage, lancer des recherches en même temps, etc., au point de saturer le système : c'est le B-A-ba d'une attaque par déni de service.

La seule solution pour éviter cela est de choisir une fonction aléatoirement à chaque instance d'une table de hachage. Ainsi les clés qui posent des problèmes seront à chaque fois différentes, et une entrée aura chaque fois une position différente dans la table. Cette manière de gérer le hachage s'appelle le hachage universel, qui donne, en moyenne, d'assez bons résultats.

Pour définir ces fonctions, on choisit un nombre premier p plus grand que n'importe quelle clé sous forme entière. On va définir la fonction de hachage-compression kitxmlcodeinlinelatexdvphfinkitxmlcodeinlinelatexdvp de la manière suivante, où M est la taille de la table, a un entier compris entre 1 et p - 1 et b un autre entier entre 0 et p - 1:

En Java, on arrive à un code similaire à celui-ci :

public class HashTable
{
    private int a, b, p;
    
    public HashTable()
    {
        p = 1073676287; // Grand nombre premier
    
        Random generator = new Random(); // Générateur de nombres aléatoires
        
        a = (abs(generator.nextInt()) % (p - 1))  + 1;
        b = abs(generator.nextInt()) % p;
    }
    
    public int hash(int k)
    {
        return abs(a * k + b) % bucketArray.length;
    }
}

Bien évidemment, le code n'est là que pour illustrer (et il faudra le travailler), mais l'idée principale est qu'à chaque instance de la table de hachage, une fonction de hachage est choisie aléatoirement et est utilisée jusqu'à ce qu'on n'ait plus besoin de l'instance.

Il est possible de choisir une fonction de double hachage de manière à vérifier au moins une fois toutes les cases de la table. Cela ne veut pas dire que vous trouverez une place libre rapidement, mais cela garantira que vous en trouverez une !
En fait, on va utiliser la propriété suivante : si la valeur de la seconde fonction de hachage est première par rapport à la taille du tableau, toutes les cases seront vérifiées.

Par exemple, prenons un tableau de 10 cases et un hash code valant 1. Une valeur possible pour la fonction de hachage est 3. Les indices parcourus seront les suivants :

Ainsi, on devra, au pire, exécuter 10 itérations de la recherche, et sans retomber une seule fois sur un indice déjà passé en revue !
Il existe plusieurs manières d'arriver à ce genre de résultat. En voici deux (tirées d'un bouquin d'algorithmique dont je parle dans la conclusion) :

• prendre comme taille de la table une puissance de 2 et s'arranger pour que kitxmlcodeinlinelatexdvph_2finkitxmlcodeinlinelatexdvp renvoie toujours une valeur impaire ;
• prendre comme taille de la table M un nombre premier et pour kitxmlcodeinlinelatexdvph_2finkitxmlcodeinlinelatexdvp utiliser une fonction qui renvoie un entier positif toujours inférieur à M, par exemple en prenant les fonctions de hachage suivantes (où M' est un nombre légèrement plus petit que la taille de la table, par exemple M - 1) :

Nous l'avons vu, chaque méthode de collision a ses avantages et inconvénients, mais elles risquent toutes de dégénérer dans certaines situations. D'où un réflexe primordial à avoir : si vous en avez la possibilité, obtenez le plus d'informations sur les données qui seront insérées dans votre table de hachage !
En effet, plus vous aurez d'infos et plus vous aurez les moyens de mieux stocker les données. Par exemple, certaines fonctions de hachage seront plus efficaces avec certains types de clés que d'autres.

Dans cette sous-partie, nous allons nous attarder sur une des données très intéressantes à connaître : le nombre de clés qui seront insérées ! En fait, les performances de votre table de hachage sont entièrement basées dessus, et il faudra tenir compte de ce nombre, que vous le connaissiez ou pas.
En effet, quelle que soit la méthode, plus il y a de clés, plus il y aura un risque de collision et plus les temps de recherche seront grands :

• avec un sondage (linéaire ou quadratique), les clusters seront de plus en plus importants ;
• avec un double hachage, de plus en plus d'itérations seront à faire ;
• avec un chaînage linéaire, les listes s'allongent.

Le fait de connaître le nombre de clés qui seront insérées peut grandement changer la donne. Par exemple, dans une situation où vous êtes obligés d'utiliser un sondage linéaire, si vous savez que vous devrez stocker 50 clés, en prenant un tableau de 100 cases, vous n'aurez pas (ou peu) de soucis à vous faire !

L'idée serait d'adapter la taille de la table en fonction du nombre de clés insérées, autrement dit l'agrandir quand il commence à être rempli (et éventuellement le rétrécir pour économiser de la place, mais nous aborderons cet aspect comme une amélioration un peu plus loin). Le tout est de savoir quand modifier la taille, et c'est dans cette optique que l'on va définir le facteur de charge.

Par définition, le facteur de charge, que je noterai par un lambda (kitxmlcodeinlinelatexdvp\lambdafinkitxmlcodeinlinelatexdvp), est le rapport entre le nombre d'éléments insérés dans la table et le nombre de cases.

Par exemple, reprenons le tableau de tout à l'heure.

Il y a 10 cases et 4 clés insérées, le rapport sera donc de 0,4. Cela s'applique aussi au chaînage linéaire.

Il y a 10 cases et 6 clés, donc le rapport sera 0,6.
Le facteur de charge est donc un indicateur du taux de remplissage de votre table : plus il est proche de 1 (100 %), moins il y aura de cases libres et donc plus les temps de recherche seront grands.

Naïvement, on pourrait penser à deux solutions violentes pour limiter le facteur :

• prendre un tableau très grand ;
• multiplier la taille du tableau à chaque insertion.

Ces solutions fonctionneront, mais ne sont vraiment pas économiques du tout. Vu qu'on ne sait pas combien de clés seront insérées, c'est relativement dangereux de fixer la taille de la table. Et si la table ne contiendra finalement que peu de clés la deuxième solution tombe à l'eau. On aura alors un gaspillage de la mémoire.

En fait, il existe une solution beaucoup plus efficace, dérivée de la seconde, et pas si compliquée à implémenter : pour chaque méthode de gestion des collisions, on va définir un facteur de charge maximum, et s'il est dépassé on agrandira la table.
Voici les valeurs que l'on m'a apprises et que j'utilise ; elles sont arbitraires et assez larges, libre à vous de les adapter ou d'essayer d'autres :

• pour un sondage et un double hachage, le facteur de charge à ne pas dépasser est 0,5 ;
• pour un chaînage linéaire, le facteur de charge à ne pas dépasser est 0,9.

Ainsi, lorsqu'on aura inséré une clé, on vérifiera le facteur de charge courant. S'il est supérieur au facteur de charge maximum, on redimensionnera la table, sinon on ne fait rien.

Nous n'allons pas faire une analyse détaillée, mais pour faire court : si

• la fonction de hachage est efficace et répartit bien uniformément les clés sur la table,
• (dans le cas du double hachage) la seconde fonction de hachage est correctement choisie,
• et si le facteur de charge est respecté

alors les tables de hachage ont un temps d'exécution constant (kitxmlcodeinlinelatexdvp\mathcal{O}(1)finkitxmlcodeinlinelatexdvp), MAIS peuvent être instables dans certains cas (par exemple avec des clés qui créent un nombre important de collisions) et avec certaines méthodes.
En termes d'espace mémoire, on a également de très bonnes performances, puisqu'on peut se limiter à un simple tableau ! Gardez cependant en tête que la méthode du chaînage linéaire utilise des listes, d'où une occupation mémoire plus grande.

Un arbre est une autre structure de données, extrêmement répandue, qui implémente aussi les tables de symboles. L'idée est également de stocker des clés et des valeurs. Seule la structure change. Nous aurons peut-être l'occasion de nous retrouver dans un autre article pour en discuter !
Pour faire court, cette structure de données organise les paires clé-valeur sous forme, je vous le donne en mille, d'arbre. Les performances sont proportionnelles à la hauteur de l'arbre : plus il est haut, plus les opérations seront lentes.

Dans certains cas la hauteur de l'arbre, pour N éléments, peut être ramenée à kitxmlcodeinlinelatexdvp\log Nfinkitxmlcodeinlinelatexdvp. Les opérations sont donc en kitxmlcodeinlinelatexdvp\mathcal{O} (\log N)finkitxmlcodeinlinelatexdvp, soit moins rapides qu'avec une table de hachage…
Mais ne criez pas victoire trop vite ! En effet, l'énorme avantage des arbres est que, quelle que soit la situation, ils sont stables et sûrs. Même des cas très pathologiques passent comme une lettre à la poste, tandis qu'il existera toujours une faille pour les tables de hachage.

De plus, certaines opérations sont compliquées ou impossibles à effectuer sur les tables de hachage, tandis qu'elles sont possibles avec les arbres. Par exemple, comme dit au début de cet article, on pourrait vouloir chercher la plus petite/grande clé, ou encore les parcourir dans l'ordre.
Cela vient du fait qu'il y a une relation d'ordre entre les nœuds d'un arbre et qu'on peut l'exploiter. Par exemple, pour un arbre binaire, la clé de tout nœud est plus grande ou égale à celle du nœud à gauche et plus petite que celle du nœud de droite. À l'opposé, la table de hachage ne définit aucun ordre entre les clés. Il faut alors procéder à des recherches exhaustives, ce qui donne des temps d'exécution abominables.