II. Pratique : implémentation en Java▲
II-A. Introduction▲
Attaquons dès à présent la seconde partie de cet article : l'implémentation concrète en Java ! En fait, on va programmer deux versions des tables de hachage :
- une première qui gère les sondages (linéaire, quadratique, double hachage) ;
- une seconde qui utilise le chaînage linéaire.
Vu que le but de ce tutoriel ne porte pas sur Java, ne vous attendez pas à une implémentation hyper efficace et profitant de toutes les fonctionnalités du langage. Il s'agit d'un choix par facilité, mais qui vous permettra de migrer aisément vers du C++, par exemple.
Un excellent exercice serait de le faire par vous-mêmes et de le corriger après !
Notez que Java possède déjà toute une panoplie de classes qui font le travail à notre place : il y a notamment une interface pour les tables de symboles et une implémentation avec du chaînage linéaire (dont vous pouvez voir le code source en cliquant ici).
Nous n'allons pas nous intéresser à ces objets, vu que le but est de recréer les tables de hachage depuis rien. Cependant, nous allons nous arranger pour utiliser notre code de la même façon. Par exemple :
HashTable<Integer,String> maTable = new HashTable<Integer,String>();
maTable.put(123, "Une valeur");
maTable.put(456, "Une autre valeur");II-B. Avant de commencer▲
Pour commencer, on va définir quelques mécanismes qui seront utilisés dans les deux versions des tables, et qui nous simplifieront la vie.
Tout d'abord, on va définir une classe qui va représenter une clé et possède une méthode de comparaison (equals) et une de hachage (hashCode). Notez que n'importe quelle classe fournie avec Java possède ces méthodes, vu qu'elles héritent toutes de la classe Object. Cependant, elles pourraient ne pas réagir comme vous le voudriez pour des classes personnalisées que vous utiliseriez comme clé.
En effet, par défaut, l'adresse interne de l'instance d'une classe « à vous » est utilisée pour le hash code et la méthode equals. Voici un exemple de comportements que cela engendre, avec une classe MonEntier toute simple :
public class MonEntier
{
private int i;
public MonEntier(int i)
{
this.i = i;
}
}Integer i1 = new Integer(5);
Integer i2 = new Integer(5);
MonEntier e1 = new MonEntier(42);
MonEntier e2 = new MonEntier(42);
boolean c1 = i1.equals(i2); // True
boolean c2 = e1.equals(e2); // False
boolean c3 = i1.hashCode() == i2.hashCode(); // True
boolean c4 = e1.hashCode() == e2.hashCode(); // FalseCes comportements peuvent être évités en réimplémentant les méthodes de test d'égalité et de génération de hash code. Si vous réutilisez des classes fournies par Java, cela est bien entendu inutile.
Par exemple, voici ce qu'il faudrait avoir pour la classe MonEntier :
public class MonEntier
{
private int i;
public MonEntier(int i)
{
this.i = i;
}
public int hashCode()
{
return i;
}
public boolean equals(Object e)
{
if(e == null || !(e instanceof MonEntier) )
return false;
MonEntier t = (MonEntier) e;
int cmp = t.i;
return (cmp == this.i);
}
}Ici, la fonction de hachage est triviale, mais pour des classes plus complexes, il serait plus intéressant de vous baser sur les fonctions de hachage vues dans la partie théorique.
Revenons à nos moutons : pour nous faciliter la vie, nous allons définir une classe conteneur pour les paires « clé-valeur » placées dans la table de hachage. Le code n'est pas spécialement compliqué :
public class Entry<K,V>
{
private K key;
private V value;
public Entry(K key, V value)
{
this.key = key;
this.value = value;
}
// Accesseurs
public K getKey() { return key; }
public V getValue() { return value; }
// Mutateurs
public void setValue(V value) { this.value = value; }
}Notez qu'il n'y a pas de mutateur pour la clé, mais bien pour la valeur. En effet, plus tard dans l'implémentation, il faudra prendre une décision concernant le cas où l'utilisateur ajoute une clé dans une table de hachage de type map qui existe déjà (alors que les clés doivent être uniques) : faut-il remplacer la valeur ou non ? Si oui, ce mutateur nous permettra de le faire facilement.
Dernière chose avant de nous lancer dans le vif du sujet : l'interface à implémenter.
public interface SymbolTable <K, V>
{
/**
* Méthode ajoutant une paire "clé-valeur" passée en argument.
*
* @param key la clé à ajouter.
* @param value l'objet à ajouter et associé à la clé.
*/
public void put(K key, V value) throws HashTableException;
/**
* Méthode récupérant l'objet associé à une clé passée en argument.
*
* @param key la clé à chercher.
* @return l'objet associé à la clé.
* @throws HashTableException si la table est vide ou si la clé n'existe
* pas dans la table.
*/
public V get(K key) throws HashTableException;
/**
* Méthode supprimant l'entrée spécifiée par la clé passée en argument.
*
* @param key la clé à supprimer.
* @return l'objet associé à la clé.
* @throws HashTableException si la table est vide ou si la clé n'existe
* pas.
*/
public V remove(K key) throws HashTableException;
/**
* Méthode vérifiant si une clé est présente dans la table de hachage.
*
* @param key la clé dont on veut vérifier la présence.
* @return vrai si la clé est présente, faux sinon.
*/
public boolean contains(K key) throws HashTableException;
/**
* Méthode retournant le nombre d'entrées dans la table.
*
* @return un entier, le nombre d'entrées dans la table.
*/
public int size();
/**
* Méthode vérifiant si la table est vide ou non.
* @return vrai si la table est vide, faux sinon.
*/
public boolean isEmpty();
}Il existe d'autres méthodes comme min, qui permettent de récupérer la clé la plus petite, mais nous n'allons pas en parler directement dans la suite de cette page, car elle n'est pas spécialement évidente à mettre en place pour des tables de hachage.
Et pour faire propre, on va définir une petite exception :
public class HashTableException extends Exception
{
public HashTableException() { super() ; }
public HashTableException(String s) { super(s); }
}II-C. Table de hachage avec sondages linéaire, quadratique et double hachage▲
II-C-1. L'entrée : un mot sur la gestion des collisions▲
La particularité du code qui va suivre est la suivante : l'utilisateur peut choisir, s'il le souhaite, la méthode de gestion des collisions. Ainsi, il pourra adapter le comportement de la table en fonction des situations… Et aussi parce que ce n'est pas spécialement plus compliqué à coder !
Pour l'instant, on ne va pas voir le code des méthodes (même s'il est simple), mais sachez que j'implémenterai l'interface suivante.
public interface CollisionManagement
{
public int nextIndex(Object key, int n, int i);
}L'idée de la méthode nextIndex est très simple : si le premier indice calculé pour une clé donne une case occupée, on va l'appeler et elle va renvoyer le prochain indice à vérifier. Voici la signification des arguments :
- Object key : la clé dont on cherche l'indice, utile pour la seconde fonction de hachage ;
- int n : la taille du tableau, pour pouvoir renvoyer un indice valable ;
- int i : l'itération à laquelle on se trouve.
Le but de la manœuvre est que, lors de l'instanciation de la table de hachage, on passe au constructeur une référence vers une classe implémentant cette interface. Par exemple, pour du sondage linéaire :
HashTable<Key, Object> h = new HashTable<Key, Object>(new LinearProbing());Dans la suite du code, j'ai fait le choix de placer la fonction de compression du hash code dans ce gestionnaire de collisions. Cela peut paraître bizarre comme choix, mais si je l'avais mis dans la clé, je n'aurais pas pu utiliser la classe Object pour la désigner (vu que cette méthode n'existe pas dedans). De plus, comme dit dans la partie théorie, ça sera plus facile pour introduire des facteurs destinés à protéger le système d'une attaque DDOS, ou encore dans le cas du double hachage, d'utiliser l'astuce pour parcourir toutes les cases.
Nous reviendrons sur ces points un peu plus loin, quand nous implémenterons les méthodes de gestion de collision.
II-C-2. Le plat de résistance : la table▲
Entrons enfin dans le vif du sujet ! La table de hachage en elle-même ne constituera qu'une seule et même classe, qui implémente l'interface SymbolTable. Au niveau des méthodes, on a donc toutes celles des tables de symboles, mais on va en ajouter une autre qui va nous simplifier grandement la vie : getBucketIndex.
En effet, dans le code une action reviendra systématiquement : celle de chercher l'emplacement d'une clé, qu'elle existe ou qu'elle n'existe pas. Ainsi, getBucketIndex va prendre en entré une clé, et, à l'aide de la fonction de hachage et du module de gestion des collisions, va retourner l'indice de la case de la table dans laquelle la clé devrait se trouver. Lorsque cette méthode sera écrite, 90% du travail sera fait !
Il ne faudra pas non plus oublier de coder une fonction de hachage, sinon on n'ira pas loin.
Au niveau des variables membres, on va définir les éléments suivants :
- un tableau d'emplacements pour des clés. Chacun de ces emplacements sera défini par une classe Bucket ;
- un entier pour compter le nombre d'objets entrés dans la table ;
- une référence vers le module de gestion des collisions (l'interface CollisionManagement).
Des variables seront rajoutées par après, nous les verrons en temps voulu. Pour l'instant, on va se contenter de remplir le code qui suit.
Notez qu'il faut prendre aussi en compte les cas où l'utilisateur n'entre pas de gestionnaire de collisions, ainsi que celui où il ne spécifie pas de taille. Pour cela, on va définir une constante qui indiquera la taille par défaut.
Je vous épargne ainsi le code des constructeurs : il ne s'agit que d'une instanciation. Par défaut, le système de gestion des collisions sera le sondage linéaire, mais libre à vous d'en mettre un autre !
public class HashTable <K,V> implements SymbolTable<K,V>
{
private Bucket<K,V>[] bucketArray; // Tableau contenant les paires "clé-valeur"
private int nbrObject = 0; // Nombre d'éléments insérés
private CollisionManagement manager; // Gestionnaire de collision
private static final int DEFAULTSIZE = 16;
public HashTable()
{
this(DEFAULTSIZE);
}
public HashTable(int size)
{
this(size, new LinearProbing());
}
public HashTable(CollisionManagement manager)
{
this(DEFAULTSIZE, manager);
}
public HashTable(int size, CollisionManagement manager)
{
this.manager = manager;
bucketArray = (Bucket<K,V>[]) new Bucket<?,?>[size];
}
public void put(K key, V value) throws HashTableException {}
public V get(K key) throws HashTableException {}
public V remove(K key) throws HashTableException {}
public boolean contains(K key) {}
public int size() {}
private int getBucketIndex(K key) {}
}II-C-2-a. La méthode getBucketIndex▲
Cette méthode va donc chercher la place d'une clé dans la table. L'algorithme se déroulera ainsi : on va récupérer le premier indice, en hachant la clé. Ensuite, on va avancer dans les indices et on s'arrêtera si un des trois cas suivants se présente :
- la case est nulle ;
- la case est un emplacement libre ;
- la case contient la clé que l'on cherche.
On va également spécifier en argument un booléen qui indique s'il faut tenir compte ou non des cases libres (c'est-à-dire avec une clé, mais qui a été supprimée). En effet, dans un cas précis (pour ne rien vous cacher à cause de la méthode put), on va rencontrer quelques problèmes. Par défaut, on ne tiendra pas compte des cases libres. Vous comprendrez ce choix bizarre dès que nous verrons le code de put.
private int getBucketIndex(K key)
{
return getBucketIndex(key, true); // Par défaut, on cherche la clé en ignorant les cases libres
}
private int getBucketIndex(K key, boolean ignoreFreeBucket)
{
int index = manager.nextIndex(key, bucketArray.length, 0); // Calcul du premier indice
for(int i = 0 ;
bucketArray[index] != null // Tant que la case n'est pas vide...
&& (!bucketArray[index].isFree() || ignoreFreeBucket) // ... ou qu'elle n'est pas libre et que cela importe
&& !key.equals(bucketArray[index].getKey()) // ... ou qu'on ne trouve pas la clé
; i++)
{
index = manager.nextIndex(key, bucketArray.length, i); // On va à la prochaine case
}
return index;
}Cette méthode est le pivot de toute la table ; comme nous allons le voir plus loin, elle sera appelée pour toute opération !
II-C-2-b. La méthode put▲
La méthode put va donc placer une clé dans la table de hachage. Il suffit d'appeler la méthode getBucketIndex, et de l'y mettre ! Pensez à envoyer une exception si la table est pleine (sauf s'il y a une méthode de redimensionnement).
public void put(K key, V value) throws HashTableException
{
if(bucketArray.length == nbrObject) // D'abord vérifier s'il reste de la place
throw new HashTableException("Table pleine.");
int index = getBucketIndex(key, false); // L'emplacement de la paire "clé-valeur"
if(bucketArray[index] == null || bucketArray[index].isFree())
nbrObject++;
bucketArray[index] = new Bucket<K,V>(new Entry<K,V>(key, value));
}Notez ici que j'ai fait un choix de conception et que si la clé que je veux insérer existe déjà dans la table, j'écraserai la valeur stockée par la nouvelle. Vous pourriez très bien faire le contraire, c'est-à-dire garder la vieille et ignorer l'ancienne, c'est à vous de décider.
De plus, pensez à ne pas incrémenter tout de suite le nombre d'éléments dans la table : c'est seulement quand la case est nulle et que la clé n'y est pas (jamais insérée ou supprimée) qu'il faut le faire.
II-C-2-c. La méthode get▲
On continue avec la méthode qui permet de récupérer une valeur en fonction de la clé. On va également utiliser la méthode getBucketIndex, le code sera tout aussi simple qu'auparavant.
On va donc d'abord récupérer l'indice de l'élément et le tester : si la case n'est pas instanciée ou si elle est libre (donc instanciée, mais où la clé a été supprimée), c'est que la clé n'est pas dans la table. Dans le cas contraire, elle y est, et on la retourne.
public V get(K key) throws HashTableException
{
if(nbrObject == 0) // Si la table est vide, cela ne sert à rien de continuer.
throw new HashTableException("Table vide.");
Bucket<K,V> bucket = bucketArray[getBucketIndex(key)]; // Case dans laquelle devrait se trouver la clé
if(bucket != null && !bucket.isFree()) // Si la case est occupée, on a trouvé notre clé !
return bucket.getValue();
else
throw new HashTableException("Clé non trouvée");
}II-C-2-d. La méthode contains▲
Cette méthode est quasiment copiée/collée de get : il suffit de calculer l'indice et de tester la case, en renvoyant vrai si elle est instanciée et occupée, faux sinon.
public boolean contains(K key) throws HashTableException
{
if(nbrObject == 0) // Si la table est vide, cela ne sert à rien de continuer.
throw new HashTableException("Table vide.");
Bucket<K,V> bucket = bucketArray[getBucketIndex(key)];
return (bucket != null && !bucket.isFree());
}II-C-2-e. La méthode remove▲
Passons à la suppression de clé, qui est calquée sur les deux méthodes précédentes : une fois qu'on a calculé l'indice avec getBucketIndex et qu'on a vérifié qu'elle contient bien la clé, on va marquer la case comme libre et retourner la valeur qui était contenue dedans.
public V remove(K key) throws HashTableException
{
if(nbrObject == 0) // Si la table est vide, cela ne sert à rien de continuer
throw new HashTableException("Table vide.");
Bucket<K,V> delete = bucketArray[getBucketIndex(key)]; // La case à nettoyer
if(delete == null || delete.isFree()) // Si la case est vide ou déjà nettoyée, on peut s'arrêter
throw new HashTableException("Clé non trouvée.");
V temp = delete.getValue(); // Valeur à retourner
delete.clean(); // On marque la case comme libre
nbrObject--;
return temp;
}II-C-2-f. Les méthodes size et isEmpty▲
Je ne vous ferai pas l'injure de commenter ces méthodes, puisqu'il n'y a qu'une variable membre à retourner/tester !
public int size()
{
return nbrObject;
}
public boolean isEmpty()
{
return (nbrObject == 0);
}II-C-3. Le dessert : implémentation des gestions de collision▲
Passons à la partie la plus amusante, qui consiste à implémenter nos méthodes de gestion de collision. Grâce à l'interface CollisionManagement et la manière dont est construite la table, cela va être un jeu d'enfant !
Nous n'avons donc qu'une seule méthode à implémenter : nextIndex. N'oubliez pas non plus qu'il faudra compresser le hash code de la clé.
public interface CollisionManagement
{
public int nextIndex(Object key, int n, int i);
}II-C-3-a. Implémentation du sondage linéaire▲
Pour rappel, le sondage linéaire a la forme suivante :
kitxmlcodelatexdvp\text{indice} = (h(k) + i) \mod MfinkitxmlcodelatexdvpDès lors, le code vient tout seul :
public class LinearProbing implements CollisionManagement
{
public int nextIndex(Object key, int n, int i)
{
int h = compression(key.hashCode(), n);
return (h + i) % n;
}
private int compression(int h, int n)
{
return h % n;
}
}II-C-3-b. Implémentation du sondage quadratique▲
On passe à un degré supérieur, avec une fonction quadratique :
kitxmlcodelatexdvp\text{indice} = (h(k) + c_1i + c_2i^2) \mod Mfinkitxmlcodelatexdvppublic class QuadraticProbing implements CollisionManagement
{
private int c1, c2;
// Si l'utilisateur ne spécifie pas les constantes lors de l'instanciation
public QuadraticProbing()
{
this(0, 1); // Ou les générer aléatoirement
}
public QuadraticProbing(int c1, int c2)
{
this.c1 = c1;
this.c2 = c2;
}
public int nextIndex(Object key, int n, int i)
{
int h = compression(key.hashCode(), n);
return (h+ c1 * i + c2 * (i * i))% n;
}
private int compression(int h, int n)
{
return h % n;
}
}Fixez les constantes quand vous instanciez la classe, ne les générez donc pas à chaque fois que vous demandez un nouvel indice, sinon on ne retrouvera jamais nos clés !
II-C-3-c. Implémentation du double hachage▲
Terminons par le double hachage :
kitxmlcodelatexdvp\text{indice} = (h(k) + ih_2(k)) \mod MfinkitxmlcodelatexdvpOn va utiliser le truc qui permet de parcourir au moins une fois toutes les cases de la table. Ce n'est pas sorcier, mais une application bête et méchante de ce qu'on a expliqué dans la partie théorie.
public class DoubleHash implements CollisionManagement
{
public int nextIndex(Object key, int n, int i)
{
int h = compression(key.hashCode(), n);
return (h + i * hash2(key, n)) % n;
}
private int compression(int h, int n)
{
return h % n;
}
private int hash2(Object key, int n)
{
int h = key.hashCode();
n--;
return 1 + (h % n);
}
}II-C-3-d. Sécurisation de la table avec le hachage universel▲
Comme nous l'avons vu dans la partie théorie, il y a moyen de se protéger d'attaques DOS élémentaires en intégrant des facteurs. Il suffit en fait de les choisir aléatoirement lorsqu'on instancie la méthode de gestion des collisions, et le tour est joué !
En effet, chaque fois que vous instancierez la table de hachage, il y aura des facteurs différents. Du coup, la (les) faille(s) qui ferai(en)t dégénérer la table sera(seront) différente(s) à chaque fois.
Je vais vous donner le code pour une seule classe, celle du sondage linéaire, mais sachez que c'est exactement la même chose pour toutes les autres.
import java.util.Random;
public class LinearProbing implements CollisionManagement
{
private int a, b, p;
public LinearProbing()
{
p = 1073676287; // Grand nombre premier
Random generator = new Random(); // Générateur de nombres aléatoires
a = (Math.abs(generator.nextInt()) % p) + 1;
b = Math.abs(generator.nextInt()) % p;
}
public int nextIndex(Object key, int n, int i)
{
int h = compression(key.hashCode(), n);
return (h + i) % n;
}
private int compression(int h, int n)
{
return Math.abs(a * h + b) % n;
}
}Notez qu'à présent, le nombre de collisions dépendra de ces facteurs choisis aléatoirement. De ce fait, pour certaines valeurs de a et b, vous aurez plus ou moins de soucis à vous faire !
II-D. Table de hachage avec chaînage linéaire▲
Attaquons la seconde implémentation des tables de hachage, avec cette fois-ci le chaînage linéaire comme méthode de gestion des collisions. Elle est séparée de la première, car le code est totalement différent.
En effet, on passe d'un tableau de valeurs à un tableau de listes. On va garder les mêmes noms de classe, mais leur job sera très différent : Bucket va ainsi gérer une liste d'instances d'une classe Node, qui constitueront les nœuds.
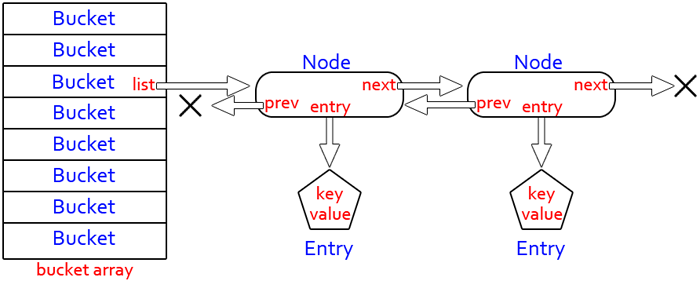
Nos classes auront l'emplacement du dessin ci-dessous :
Les noms en bleu sont les classes, ceux en rouge sont les variables et les flèches sont des références. Notez que la classe Entry ne change pas, vu qu'elle ne dépend pas de l'implémentation.
II-D-1. La classe Node▲
Il s'agit d'un nœud de liste doublement liée classique, avec une référence vers la case précédente, une autre vers la suivante, et une référence vers le conteneur Entry.
Pour universaliser le tout, on va paramétrer la classe du conteneur, pour éventuellement réutiliser le nœud plus tard.
public class Node<E>
{
private E entry;
private Node<E> next, prev; // Noeuds précédent et suivant
public Node(E entry)
{
this(entry, null);
}
public Node(E entry, Node<E> next)
{
this.entry = entry;
this.next = next;
this.prev = null;
}
// Accesseurs
public E getEntry() { return entry; }
public Node<E> getNext() { return next; }
public Node<E> getPrev() { return prev; }
// Mutateurs
public void setNext(Node<E> next) { this.next = next; }
public void setPrev(Node<E> prev) { this.prev = prev; }
}Notez que le premier constructeur va créer un nœud « seul », sans lien vers un autre, tandis que le second va, lui, définir un nœud suivant. Cela nous servira pour la classe Bucket quand on ajoutera un nœud dans la liste.
II-D-2. La classe Bucket▲
La classe Bucket va donc gérer une liste. On va y implémenter des méthodes qui permettent d'ajouter, de chercher et de supprimer un nœud en connaissant la clé qu'il contient.
En variable membre, on va retenir le nombre de nœuds qui ont été insérés et le premier nœud de la liste. On va implémenter les méthodes suivantes :
public class Bucket<K,V>
{
private int nbrNode = 0;
private Node<Entry<K,V>> list; // Tête de liste
public Bucket(Entry<K,V> e)
{
this.addNode(e);
}
public Node<Entry<K,V>> getFirstNode() {}
public boolean addNode(Entry<K,V> e) {}
public V removeNode(K key) throws HashTableException {}
public Node<Entry<K,V>> getNode(K key) {}
public boolean containsNode(K key) {}
public int getNbrNode() {}
}Elles seront toutes utilisées par la classe HashTable. On passera sur la méthode qui retourne le nombre de nœuds et le constructeur, vu qu'ils sont très simples.
II-D-2-a. La méthode getNode▲
On va commencer par la méthode getNode, car elle sera réutilisée quasiment partout. Son rôle est de renvoyer le nœud qui contient la clé qu'on lui passe en argument.
Pour y parvenir, elle va parcourir la liste (dont le premier élément est la variable membre list) : tant qu'on n'est pas en dehors de la liste ou qu'on n'est pas tombé sur la clé, on avance en utilisant la variable membre next des nœuds.
public Node<Entry<K,V>> getNode(K key)
{
Node<Entry<K,V>> n = list;
/* Tant qu'on n'a pas la clé ou qu'on n'est pas dans un noeud vide,
on avance dans la liste */
while(n != null && !n.getEntry().getKey().equals(key))
n = n.getNext();
return n;
}II-D-2-b. La méthode addNode▲
Comme son nom l'indique, addNode est une méthode qui va ajouter dans la liste un nœud avec une nouvelle entrée, et qui va retourner vrai s'il a bien été ajouté. En effet, il faut garder en tête que si la clé est déjà présente dans la liste, le nombre total de clés (la variable nbrObject dans la classe HashTable) n'augmente pas.
Pour raccourcir le code, on va systématiquement ajouter le nœud au début de la liste, en vérifiant auparavant si elle n'est pas vide (list == null).
public boolean addNode(Entry<K,V> e)
{
if(list == null)
{
list = new Node<Entry<K,V>>(e);
nbrNode++;
return true;
}
Node<Entry<K,V>> n = getNode(e.getKey());
if(n != null) // Si la clé est déjà dans la liste, on change la valeur
{
n.getEntry().setValue(e.getValue());
return false;
}
// Si la clé n'est pas dans la liste, on ajoute un noeud
nbrNode++;
Node<Entry<K,V>> v = new Node<Entry<K,V>>(e, list); // Nouveau noeud, future tête de liste
if(list != null) // S'il y a déjà un noeud en tête, on met à jour la référence prev
list.setPrev(v);
list = v; // Mise à jour de la tête de liste
return true;
}II-D-2-c. La méthode removeNode▲
La méthode removeNode va supprimer le nœud dont la clé est spécifiée en argument, et renvoyer la valeur associée.
La difficulté vient surtout des références previous et next, qu'il faut modifier sans se tromper !
public V removeNode(K key) throws HashTableException
{
Node<Entry<K,V>> n = getNode(key);
if(n == null)
throw new HashTableException("Clé non trouvée.");
V temp = n.getEntry().getValue();
nbrNode--;
if(n.getPrev() != null) // Si le noeud est dans la liste
n.getPrev().setNext(n.getNext());
else // Si le noeud est le premier de la liste
list = n.getNext();
if(n.getNext() != null)
n.getNext().setPrev(n.getPrev());
return temp;
}II-D-2-d. La méthode containsNode▲
Pour savoir si la liste contient la clé, il suffit de tester le retour de getNode.
public boolean containsNode(K key)
{
return (getNode(key) != null);
}II-D-3. La classe HashTable▲
On arrive enfin à la partie amusante ! Tout ce que nous allons faire est de la manipulation de listes.
On va cependant se retrouver confronté à un « petit » problème : vu qu'il n'y a qu'un seul moyen de gérer les collisions, on n'a pas besoin de module de gestion des collisions (l'interface CollisionMangement). Or, c'est ce module qui se charge de donner l'indice en hachant et compressant la clé.
On va donc définir deux méthodes privées, une qui va donner l'indice d'une clé et une autre qui va compresser le hash code.
private int getIndex(K key)
{
return compress(key.hashCode());
}
private int compress(int h)
{
return h % bucketArray.length;
}Bien évidemment, vous pouvez utiliser le code de hachage universel de la section précédente.
II-D-3-a. La méthode put▲
Pour put, il faut d'abord trouver la liste dans laquelle doit s'ajouter la paire avec la méthode getIndex. Ensuite, on a deux cas :
- la liste n'existe pas (null) : on l'instancie, avec comme premier élément la paire qu'on veut ajouter ;
- la liste existe déjà : on appelle la méthode d'ajout de nœud.
Bref, de l'application bête et méchante. La difficulté vient juste de savoir quand une paire est ajoutée ou non. Et c'est là que le booléen que retourne la méthode addNode entre en jeu : si la clé est effectivement ajoutée (c'est-à-dire si la clé n'existait pas déjà et si elle n'a pas été remplacée), on incrémentera.
public void put(K key, V value)
{
int index = getIndex(key);
Entry e = new Entry(key, value);
if(bucketArray[index] != null) // Si la liste est instanciée
{
if(bucketArray[index].addNode(e))
nbrObject++;
}
else
{
bucketArray[index] = new Bucket<K,V>(e);
nbrObject++;
}
}II-D-3-b. La méthode get▲
Ici encore, on récupère la liste de la clé, puis on appelle la méthode getNode et on teste le retour : s'il est à null, la clé n'existe pas, sinon on retourne la valeur. Bien entendu, il faut vérifier que la liste est instanciée, sinon la clé n'existera pas non plus.
public V get(K key) throws HashTableException
{
// Si la table est vide, on ne trouvera jamais notre clé
if(nbrObject == 0)
throw new HashTableException("Table vide.");
int index = getIndex(key);
// Si la liste n'est pas instanciée ou est vide, on s'arrête également
if(bucketArray[index] == null || bucketArray[index].getNbrNode() == 0)
throw new HashTableException("Clé non trouvée");
Node<Entry<K,V>> n = bucketArray[index].getNode(key);
// Si le noeud existe, on retourne la valeur
if(n != null)
return n.getEntry().getValue();
else
throw new HashTableException("Clé non trouvée.");
}II-D-3-c. La méthode contains▲
Encore une fois, on fait appel aux méthodes de gestion de liste, ce qui rend le code très simple ! Il suffit de récupérer le nœud et de vérifier s'il existe ou non.
public boolean contains(K key)
{
if(nbrObject == 0)
return false;
int index = getIndex(key);
Bucket<K,V> b = bucketArray[index];
// Retourne vrai si la liste existe et contient un noeud de clé key
return (b != null && b.containsNode(key));
}II-D-3-d. La méthode remove▲
Comme pour les autres méthodes, remove se résume à appeler removeNode à la case de l'indice généré par le hash code, sans oublier les sempiternelles vérifications.
public V remove(K key) throws HashTableException
{
if(nbrObject == 0)
throw new HashTableException("Table vide.");
int index = getIndex(key);
if(bucketArray[index] == null)
throw new HashTableException("Clé non trouvée.");
nbrObject--;
return bucketArray[index].removeNode(key);
}II-E. Intégration du facteur de charge▲
Notre code est bien beau… mais la table sera inutilisable lorsqu'elle sera remplie ! On va donc y intégrer le facteur de charge qui, comme présenté dans la partie théorique, va permettre de redimensionner la table.
L'avantage est que le code est presque le même pour les sondages et le chaînage, seul un bout diffère.
Nous allons donc définir une méthode resize qui va s'occuper de l'agrandissement de la table, si le facteur de charge est dépassé. D'ailleurs, on va commencer par définir ce dernier, sous forme d'une constante.
On peut déjà placer l'appel à la méthode dans la méthode put, et seulement dans celle-ci, vu que c'est la seule susceptible d'engendrer un dépassement.
private static final float MAXLOADFACTOR = 0.5f;
private void resize() throws HashTableException
{
// ...
}public void put(K key, V value) throws HashTableException
{
// Redimensionner la table si nécessaire
resize();
int index = getBucketIndex(key, false); // L'emplacement de la paire "clé-valeur"
if(bucketArray[index] == null || bucketArray[index].isFree())
nbrObject++;
bucketArray[index] = new Bucket<K,V>(new Entry<K,V>(key, value));
}Notez qu'il est à présent inutile de vérifier si la table est pleine… puisqu'elle ne le sera jamais !
II-E-1. Cas des sondages▲
Pour rappel, le facteur de charge est le rapport entre le nombre d'objets insérés et la taille de la table. Une petite division suffit, suivie d'une comparaison.
La stratégie que j'ai suivie est de créer une nouvelle table de hachage plus grande, et d'y insérer toutes les entrées de la table à redimensionner. Il suffira ensuite de mettre à jour la référence de la table, et le tour sera joué.
float loadFactor = (float) nbrObject / bucketArray.length;
if(loadFactor >= MAXLOADFACTOR)
{
int t = (int) (bucketArray.length * 1.5); // Nouvelle taille
HashTable<K,V> tmp = new HashTable<K,V>(t, management);
/* Récupérer les entrées et les insérer dans tmp */
bucketArray = tmp.bucketArray;
}Vous êtes bien évidemment libre de choisir la nouvelle taille que vous voulez, sans prendre une taille plus petite, sinon vous allez entrer dans une boucle de redimensionnements sans fin. Par contre, n'oubliez surtout pas de spécifier le type de gestion des collisions, sinon il y aura des inconsistances !
Prenez garde à la taille par défaut de la table de hachage ! En effet, si elle est trop petite, lors du redimensionnement, le programme peut planter purement et simplement. Par exemple, si par défaut la taille est de 4 cases, et que vous augmentez la taille d'un facteur 1.2, vous obtiendrez lors du premier redimensionnement 4.8, autrement dit 4 lors de la conversion vers un entier. Ce phénomène se reproduira pour les prochaines tentatives de redimensionnement, la table ne s'agrandira jamais.
Veillez donc à bien choisir une taille par défaut qui ne crée pas ce genre d'incident, mais également à vérifier la valeur qu'un utilisateur peut spécifier via un constructeur.
Pour les sondages, il suffit de parcourir le tableau : si la case est instanciée et non libre, on ajoute la clé et la valeur dans la table temporaire.
for(int i = 0 ; i < bucketArray.length ; i++)
{
Bucket<K,V> b = bucketArray[i];
if(b != null && !b.isFree())
tmp.put(b.getKey(), b.getValue());
}II-E-2. Le cas du chaînage linéaire▲
Le code de calcul et de création de la nouvelle table de hachage est exactement le même, si ce n'est qu'il ne faut pas spécifier de méthode de gestion des collisions dans le constructeur de cette dernière. Seul le code de parcours est à adapter.
Pour nous faciliter grandement la vie, on va définir une méthode removeFirstNode dans la classe Bucket, et qui va retourner le premier nœud de la liste tout en le supprimant. Ainsi, on n'aura qu'à itérer sur le nombre de nœuds de l'alvéole ; tant qu'il y aura des nœuds, on retirera le premier et on l'ajoutera dans la nouvelle table.
Le code est très similaire à la suppression de n'importe quel nœud, si ce n'est qu'on retire le nœud de tête. Il va donc falloir redéfinir le nœud de tête (s'il existe) et mettre à jour la référence du nœud précédent, pour autant que ces nœuds existent.
public Node<Entry<K,V>> removeFirstNode()
{
if(list == null || nbrNode == 0)
return null;
/* Mise à jour de la référence du second élément de la liste, pour
* autant qu'il existe. */
Node<Entry<K,V>> newList = list.getNext();
if(newList != null)
newList.setPrev(null);
// Le noeud à retourner, pour ne pas perdre la référence
Node<Entry<K,V>> firstNode = list;
// Mise à jour du noeud de tête
list = newList;
nbrNode--;
return firstNode;
}Le code pour le redimensionnement devient alors extrêmement simple, puisqu'il suffit d'itérer sur le nombre de nœuds et de retirer chaque fois le premier nœud, tant qu'il y en a, et ce pour chaque alvéole de la table.
for(int i = 0 ; i < bucketArray.length ; i++)
{
Bucket<K,V> b = bucketArray[i];
if(b == null)
continue;
while(b.getNbrNode() > 0)
{
Node<Entry<K,V>> n = b.removeFirstNode();
tmp.put(n.getEntry().getKey(), n.getEntry().getValue());
}
}II-F. Conclusion▲
C'est sur cette implémentation que se termine cet article sur les tables de hachage ; vous pouvez retrouver tous les fichiers (avec de la Javadoc) dans cette archive. Un grand merci à khayyam qui m'a invité à le publier, ainsi qu'à ceux qui m'ont conseillé et aidé pour cette première publication. Il serait injuste de ne pas citer ced, qui a passé son temps à corriger cet article, merci à lui !
Si vous souhaitez approfondir la matière, je peux vous recommander deux livres très intéressants :
- Data Structures and Algorithms in Java, un livre sur les structures de données en Java (la fonction de hachage cyclique vient de là) ;
- Introduction à l'algorithmique, qui va un peu plus loin que le premier, en français.
Sur ce, bonne lecture et à bientôt dans un prochain article !