Les piles, files et deques
Date de publication : 26 août 2011.
Par
Jean-Philippe Collette (http://jipe.developpez.com/)
Dans cet article, nous allons explorer trois structures de données de base : les piles, les files et les deques.
Aucun pré-requis n'est nécessaire. Bonne lecture !
I. Introduction
II. Les piles
II-A. Le type de donnée abstrait
II-B. Implémentations
II-B-1. Avec un tableau
II-B-1-a. Pseudo-code
II-B-1-b. Performances
II-B-2. Avec une liste liée
II-B-2-a. Pseudo-code
II-B-2-b. Performances
II-C. Implémentations en Java
II-C-1. Avec un tableau
II-C-1-a. Constructeurs et variables membres
II-C-1-b. La méthode push
II-C-1-c. La méthode top
II-C-1-d. La méthode pop
II-C-2. Avec une liste liée
II-C-2-a. Constructeurs et variables membres
II-C-2-b. La méthode push
II-C-2-c. La méthode top
II-C-2-d. La méthode pop
III. Les files
III-A. Le type de donnée abstrait
III-B. Implémentations
III-B-1. Avec un tableau
III-B-2. Avec une liste liée
III-C. Implémentations en Java
III-C-1. Avec un tableau
III-C-1-a. Constructeurs et variables membres
III-C-1-b. La méthode offer
III-C-1-c. La méthode peek
III-C-1-d. La méthode poll
III-C-2. Avec une liste liée
III-C-2-a. Constructeurs et variables membres
III-C-2-b. La méthode offer
III-C-2-c. La méthode peek
III-C-2-d. La méthode poll
IV. Les deques
I. Introduction
Dans cet article, nous allons explorer trois structures de données que tout programmeur aura l'occasion d'utiliser un jour ou l'autre.
Ces structures permettent donc de stocker des éléments et de les récupérer. On distingue deux politiques dans cette procédure d'ajout et de retrait :
- la politique LIFO, pour Last In, First Out, et
- la politique FIFO, pour First In, First Out.
Lorsque la structure est dite LIFO, cela signifie que le dernier élément inséré sera le premier élément qui sera extrait. Une analogie bien connue est celle d'une pile de crêpes : pendant la cuisson, vous les empilez les unes au-dessus des autres, et lorsque vous les mangez, vous commencez par la dernière qui a été cuite.
Ce comportement est adopté par les piles.
La politique FIFO est légèrement différente : le premier élément inséré sera le premier à être extrait. Une analogie très simple est celle d'une caisse de super-marché : c'est le premier client arrivé qui sera le premier servi.
Ce comportement est, vous vous en doutez maintenant, adopté par les files.
Un deque est une sorte d'hybride : il permet d'ajouter des éléments qui seront au début ou à la fin, lorsqu'on voudra les extraire. Nous y reviendrons par après, il vaut mieux avoir vu les deux premières structures avant de s'y attaquer.
II. Les piles
Comme dit ci-dessus, une pile est une structure de données avec la politique LIFO ; le dernier élément inséré sera le premier à en sortie.
Une pile s'utilise dans énormément de situations différentes. En voici quelques-unes.
- Dans les éditeurs de texte, on utilise souvent les fonctions d'annulation et de rétablissement, qui permettent d'annuler ou de réexécuter des opérations (insérer des caractères, changer la police, mettre en gras, etc). Pour implémenter ces fonctions, on peut déclarer deux piles et définir des opérations de base de modification de texte. Chaque fois qu'une telle opération est effectue, on la place dans une des piles, qui contiendra les actions précédemment exécutées. Pour annuler la dernière opération, il suffit de récupérer la dernière qui a été insérée (top()), d'effectuer l'action contraire, puis de la placer dans l'autre pile (qui contiendra les opérations qui ont été rétablies). Idem pour les rétablissements : en vidant la seconde pile, vous rétablirez toutes les opérations que vous avez effectuées.
- Ce qui est valable pour les éditeurs de texte l'est aussi pour les web browser : chaque fois que vous visitez une page, l'URL est placée dans dans une pile, et le même mécanisme est appliqué lorsque vous cliquez sur les boutons pour accéder aux pages précédente/suivante.
- En assembleur, la pile est la structure incontournable : elle permet les appels de fonction avec arguments, la récursion, d'avoir des variables en mémoire et non dans des registres, etc.
II-A. Le type de donnée abstrait
Voici les méthodes principales d'une pile :
- push(élément) : insère un élément au sommet de la pile ;
- top() : retourne l'élément au sommet de la pile ;
- pop() : idem que top, mais supprime l'élément en tête.
Quand nous nous attaquerons à l'implémentation en Java, nous implémenterons l'interface suivante.
public interface Stack<E> {
public void push(E element);
public E top() throws StackException;
public E pop() throws StackException;
public int size();
}
|
L'exception StackException permet de ne pas renvoyer une valeur particulière lorsque la pile est vide. On pourrait très bien renvoyer null, c'est à vous de choisir.
Pour les intéressés, voici le code de l'exception.
public class StackException extends Exception {
public StackException() { super(); }
public StackException(String m) { super(m); }
}
|
II-B. Implémentations
Il existe deux méthodes pour implémenter une pile (ainsi qu'une file, nous y reviendrons) : en utilisant un tableau ou une structure liée.
II-B-1. Avec un tableau
L'idée est de placer dans le tableau les éléments, l'un à la suite de l'autre, dans l'ordre dans lequel ils sont insérés. Ausi, lorsqu'on effectura un pop() (ou un top()), il suffira de retourner le dernier élément du tableau ! Cela peut se faire très facilement avec un entier qui indiquera combien d'éléments ont été insérés ; l'indice du dernier élément inséré sera le nombre d'éléments insérés - 1.
L'avantage de l'implémentation avec un tableau est qu'elle est très simple, cependant il faudra gérer le cas où le tableau sera plein. Il sera alors nécessaire d'instancier un tableau plus grand, et de tout recopier dedans.
II-B-1-a. Pseudo-code
Nous allons commencer par la méthode d'insertion, push(). Elle prend comme argument un élément e. La variable nbrObject, comme son nom l'indique, compte le nombre d'éléments qui ont été insérés dans la pile, et est initialisée à 0.
Il suffit donc d'utiliser cette dernière pour insérer l'élément à la fin du tableau, à la suite des autres éléments. Bien évidemment, avant de l'ajouter, il faudra vérfier s'il reste de la place dans le tableau ; je ne met aucun code à cet effet, c'est à vous de gérer cela selon le langage choisi.
PUSH(e)
DEBUT
array[nbrObject] = e
nbrObject <- nbrObject + 1
FIN
|
Passons à top() : il faut retourner le dernier élément inséré, récupérable facilement en connaissant le nombre d'éléments insérés.
TOP()
DEBUT
RENVOYER array[nbrObject - 1]
FIN
|
Reste pop() qui, en plus de retourner le dernier élément, le supprime.
POP()
DEBUT
nbrObject <- nbrObject - 1
RENVOYER array[nbrObject]
FIN
|
II-B-1-b. Performances
Dans la plupart des cas, l'implémentation avec un tableau sera, au niveau de l'exécution, en temps constant (
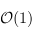
), sauf lorsqu'il y a une redimension. Dans ce cas, le temps sera linéaire (
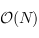
, avec
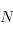
le nombre d'éléments dans la pile).
Cependant, vu qu'on aura beaucoup plus de cas constants que linéaires, on peut considérer que le temps, en complexité amortie, est constant.
En terme d'espace mémoire, la complexité est linéaire : il n'y a qu'un tableau unidimensionnel qui sera nécessaire.
II-B-2. Avec une liste liée
On peut remplacer le tableau par une liste liée, mais avec un ordre différent : chaque fois qu'on insère un élément dans la pile, on l'ajoute au début de la liste (et non à la fin, comme pour un tableau). A chaque pop() ou top(), il suffira également d'accéder au premier élément (via un pointeur/une référence).
Utiliser une liste liée comporte un énorme avantage : on ne sera jamais embêté par un problème de capacité, aucun redimensionnement ne sera nécessaire !
Par contre, vous devrez gérer une structure pour les noeuds de la liste, avec un pointeur/une références vers le noeud suivant. Vous pourriez même en utiliser un autre pointeur/une autre référence pour atteindre le noeud précédent, afin d'avoir une liste doublement liée. Cependant, dans le cas qui nous occupe, cela n'est pas nécessaire, nous n'en parlerons pas dans cet article.
II-B-2-a. Pseudo-code
On va supposer qu'on dispose d'un pointeur head vers le premier élément de la liste, pour peu qu'elle ne soit pas vide.
push() va donc ajouter un élément en tête de la file.
PUSH(e)
DEBUT
n <- NOUVEAU_NOEUD(e)
n.next <- head
head <- n
FIN
|
La méthode top() va retourner le premier élément de la liste, ou bien nil si elle est vide.
TOP()
DEBUT
SI head = nil ALORS
RENVOYER nil
SINON
RENVOYER head.element
FIN SI
FIN
|
Terminons par pop(), qui modifira le pointeur de la tête de file.
POP()
DEBUT
SI head = nil ALORS
RENVOYER nil
SINON
tmp <- head.element
head <- head.next
RENVOYER tmp
FIN SI
FIN
|
II-B-2-b. Performances
En complexité temporelle, toutes les opérations seront en temps constant ; seuls des changements de pointeur/référence sont à effectuer sur la tête de la liste.
La complexité spatiale est quant à elle linéaire, mais l'implémentation sera logiquement un peu plus lourde que celle avec un tableau, à cause de la structure des noeuds. Maintenant, ce n'est certainement pas cela qui va tripler l'utilisation mémoire de votre pile !
II-C. Implémentations en Java
Nous allons implémenter l'interface suivante.
public interface Stack<E> {
public void push(E element);
public E top() throws StackException;
public E pop() throws StackException;
public int size();
}
|
Java intègre déjà une implémentation d'une interface de pile, la classe
 Stack
Stack ; elle est légèrement différente de celle que nous allons implémenter, mais les principales méthodes s'y trouvent.
 |
Je ne rentrerai pas dans les détails de l'implémentation de la pile en elle-même, cela serait recopier ce que j'ai déjà dit pour le pseudo-code. Seul l'aspect Java sera abordé, mais vu la simplicité du code, ne vous attendez pas à un roman fleuve.
|
II-C-1. Avec un tableau
La première étape va être de définir un conteneur, qui représentera une case dans le tableau. Elle est très simple, puisqu'elle ne possède qu'un accesseur et un mutateur.
Nous allons cependant anticiper un peu, et définir une méthode swapElement, qui prend un nouvel élément en argument, qui remplace l'ancien élément par le nouveau, et qui renvoie l'ancien.
public class Bucket<E> {
private E element;
public Bucket() {
this(null);
}
public Bucket(E element) {
this.element = element;
}
public E getElement() {
return this.element;
}
public void setElement(E element) {
this.element = element;
}
public E swapElement(E element) {
E tmp = this.element;
this.element = element;
return tmp;
}
}
|
II-C-1-a. Constructeurs et variables membres
Commençons par le commencement : vu que l'implémentation est basée sur un tableau, nous allons en instancier un, à base de Buckets. Nous allons également garder le nombre d'éléments insérés dans la pile, via nbrObject.
Enfin, dans un grand élan de générosité, nous allons permettre à l'utilisateur de choisir la taille de base de la pile. Il vaut cependant définir une taille par défaut, si elle n'est pas spécifiée. Elle servira également de valeur minimale, au cas où une taille trop faible (voir négative) serait entrée.
Vu que nous allons manipuler un tableau, il faut parer à la situation où il est plein. C'est la raison d'être de la méthode resize() : s'il n'y a plus de place disponible, elle va doubler la taille du tableau (en conservant, bien évidemment, les données précédemment insérées).
Cela nous donne le code Java suivant :
public class StackArray<E> implements Stack<E> {
private Bucket<E>[] array;
private static final int DEFAULTSIZE = 16;
private int nbrObject = 0;
public StackArray() {
this(DEFAULTSIZE);
}
@SuppressWarnings("unchecked")
public StackArray(int size) {
this.array = (Bucket<E>[]) new Bucket<?>[Math.max(DEFAULTSIZE, size)];
}
public int size() {
return nbrObject;
}
private void resize() {
int l = array.length;
if(l > nbrObject)
return;
Bucket<E>[] tmp = (Bucket<E>[]) new Bucket<?>[2 * l];
for(int i = 0 ; i < l ; i++)
tmp[i] = array[i];
array = tmp;
}
public void push(E element) {
}
public E pop() throws StackException {
}
public E top() throws StackException {
}
}
|
II-C-1-b. La méthode push
Le code est exactement le même que dans le pseudo-code, avec l'appel à la méthode de redimensionnement en plus.
public void push(E element) {
resize();
array[nbrObject] = new Bucket(element);
nbrObject++;
}
|
II-C-1-c. La méthode top
Rien de particulier non plus, si ce n'est l'exception retournée si la pile est vide. Notez que vous pouvez tout aussi bien retourner null, ce n'est qu'un choix d'implémentation.
public E top() throws StackException {
if(nbrObject == 0)
throw new StackException("Empty stack");
return array[nbrObject - 1].getElement();
}
|
II-C-1-d. La méthode pop
Le pseudo-code est similaire à ce qui suit.
public E pop() throws StackException {
E tmp = top();
nbrObject--;
return tmp;
}
|
II-C-2. Avec une liste liée
Passons à la seconde implémentation, avec une liste liée. On va avoir également besoin d'un conteneur, qui représentera un noeud dans une liste liée.
public class Node<E> {
private E element;
private Node<E> prev, next;
public Node() {
this(null);
}
public Node(E element) {
this.element = element;
this.prev = null;
this.next = null;
}
public void setNext(Node<E> n) {
this.next = n;
}
public void setPrevious(Node<E> p) {
this.prev = p;
}
public Node<E> getNext() {
return next;
}
public Node<E> getPrevious() {
return prev;
}
public E getElement() {
return this.element;
}
public void setElement(E element) {
this.element = element;
}
public E swapElement(E element) {
E tmp = this.element;
this.element = element;
return tmp;
}
}
|
II-C-2-a. Constructeurs et variables membres
Blablabla
public class StackList<E> implements Stack<E> {
private Node<E> head = null;
private int nbrObject = 0;
public StackList() {
}
public int size() {
return nbrObject;
}
public void push(E element) {
}
public E pop() throws StackException {
}
public E top() throws StackException {
}
}
|
II-C-2-b. La méthode push
public void push(E element) {
Node<E> n = new Node<E>(element);
n.setNext(head);
head = n;
nbrObject++;
}
|
II-C-2-c. La méthode top
public E top() throws StackException {
if(nbrObject == 0)
throw new StackException("Empty stack");
return head.getElement();
}
|
II-C-2-d. La méthode pop
public E pop() throws StackException {
E tmp = top();
head = head.getNext();
nbrObject--;
return tmp;
}
|
III. Les files
III-A. Le type de donnée abstrait
III-B. Implémentations
III-B-1. Avec un tableau
III-B-2. Avec une liste liée
III-C. Implémentations en Java
III-C-1. Avec un tableau
III-C-1-a. Constructeurs et variables membres
public class QueueArray<E> implements Queue<E> {
private Bucket<E>[] array;
private static final int DEFAULTSIZE = 16;
private int nbrObject = 0;
private int head = 0;
public QueueArray() {
this(DEFAULTSIZE);
}
@SuppressWarnings("unchecked")
public QueueArray(int size) {
this.array = (Bucket<E>[]) new Bucket<?>[Math.max(DEFAULTSIZE, size)];
}
public int size() {
return nbrObject;
}
private void resize() {
int l = array.length;
if(l > nbrObject)
return;
Bucket<E>[] tmp = (Bucket<E>[]) new Bucket<?>[2 * l];
for(int i = 0 ; i < l ; i++)
tmp[i] = array[(head + i)%l];
array = tmp;
head = 0;
}
public void offer(E element) {
}
public E poll() throws QueueException {
}
public E peek() throws QueueException {
}
}
|
III-C-1-b. La méthode offer
public void offer(E element) {
resize();
array[nbrObject] = new Bucket(element);
nbrObject++;
}
|
III-C-1-c. La méthode peek
public E peek() throws QueueException {
if(nbrObject == 0)
throw new QueueException("Empty queue");
return array[head].getElement();
}
|
III-C-1-d. La méthode poll
public E poll() throws QueueException {
E tmp = peek();
head++;
nbrObject--;
return tmp;
}
|
III-C-2. Avec une liste liée
III-C-2-a. Constructeurs et variables membres
public class QueueList<E> implements Queue<E> {
private Node<E> head = null, tail = null;
private int nbrObject = 0;
public QueueList() {
}
public int size() {
return nbrObject;
}
public void offer(E element) {
}
public E poll() throws QueueException {
}
public E peek() throws QueueException {
}
}
|
III-C-2-b. La méthode offer
public void offer(E element) {
Node<E> n = new Node<E>(element);
if(tail != null)
tail.setNext(n);
tail = n;
if(head == null)
head = n;
nbrObject++;
}
|
III-C-2-c. La méthode peek
public E peek() throws QueueException {
if(nbrObject == 0)
throw new QueueException("Empty queue");
return head.getElement();
}
|
III-C-2-d. La méthode poll
public E poll() throws QueueException {
E tmp = peek();
head = head.getNext();
nbrObject--;
return tmp;
}
|
IV. Les deques


Les sources présentées sur cette page sont libres de droits
et vous pouvez les utiliser à votre convenance. Par contre, la page de présentation
constitue une œuvre intellectuelle protégée par les droits d'auteur. Copyright ©
2011 Jean-Philippe Collette. Aucune reproduction, même partielle, ne peut être
faite de ce site ni de l'ensemble de son contenu : textes, documents, images, etc.
sans l'autorisation expresse de l'auteur. Sinon vous encourez selon la loi jusqu'à
trois ans de prison et jusqu'à 300 000 € de dommages et intérêts.
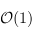 ), sauf lorsqu'il y a une redimension. Dans ce cas, le temps sera linéaire (
), sauf lorsqu'il y a une redimension. Dans ce cas, le temps sera linéaire (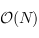 , avec
, avec 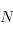 le nombre d'éléments dans la pile).
le nombre d'éléments dans la pile). Stack ; elle est légèrement différente de celle que nous allons implémenter, mais les principales méthodes s'y trouvent.
Stack ; elle est légèrement différente de celle que nous allons implémenter, mais les principales méthodes s'y trouvent.
